What is a Triangle?

Triangle is a figure that consists of three edges and three vertices. To make a triangle we need to draw three straight lines and join them together. The sum of all the angles of the triangle adds up to 180 °. This is common for all the different types of triangles that we are going to learn about in this Blog today.

What is a Vertex?

A point where two sides of a triangle meet is called the vertex of the triangle. In the below △ ABC sides AB and BC are intersected at point B, therefore, B is called the vertex. Similarly, sides AC and BC are intersected at point C, so C is the vertex, and for sides AB and AC, the vertex is A.

Different Types of Triangles

As we have read earlier, the sum of all the angles of the triangle is 180 °, but, does that mean that all triangles look the same? In Geometry, there are three main classifications of triangles which are as follows:

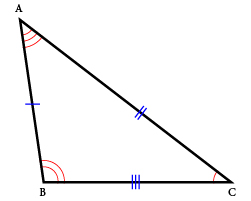
Scalene Triangle

In a scalene triangle, all sides of the triangle are of different measures. If you take a ruler and check the length of sides AB, AC, and CB, you will notice that each one has a different measure. Also, all the angles of the scalene triangle are different degrees. Use a protractor to measure the angles and you will find that the angles are also different, though their sum is 180 °.

Isosceles Triangle

In an isosceles triangle, two sides are equal and the length of the third side is not the same as the other two. In the below diagram sides, DE and EF are of the same length and thus it is categorized as an isosceles triangle. Notice the interior angles of the triangle below? Theory states that the angles opposite to the equal sides of the isosceles triangle are of equal degrees. In △ DEF, where sides DE and EF are of equal length, ∠D = ∠F (vertex D and vertex F are of the same degree)

Equilateral Triangle

As the name suggests, an equilateral triangle has equal sides and qual measure of angles. Each of the interior angles measures 60 °. In △ PQR, sides PQ, QR, and PR are of the same size, and ∠P = ∠Q = ∠R = 60°.

As an educator, you must be wondering how to teach kids ‘types of triangles’ in an engaging manner, such that they remember the concepts thoroughly. Well, the Mathletics online platform integrates the same curriculum of International Schools in the Middle East & around the world, to offer well-researched modules to students. Learners can first access the resources to understand the basic concept and then put their skills to test by engaging in over 1200 activities. To learn more about Mathletics and its availability in the UAE region, simply visit this Link: https://knowledge-hub.com/mathletics/

Classification by types of Angles

With reference to angles, triangles can be further classified as; Acute angle, obtuse angle, and right angle.

Acute Angle

An acute angle is recognized when its internal angles are less than 90 °. That means the angle can be anything like; 45°, 30°, 83 ° and so on, unless it is lesser than 90°. In the below figure, the angle formed at the intersection of Ray 1 and Ray 2 is 60° which is lesser than 90° and hence it forms an acute angle.

Obtuse Angle

An obtuse angle is defined when the degree of the angle is more than 90 °, but less than 180°. In the figure, Ray 1 and Ray 2 intersect at vertex Y which is 120° and thus greater than 90 ° & lesser than 180 °, indicating it is an obtuse angle. Practice your Math concepts in a game-like program through the Mathletics platform whose trial version is available for Free to all in Dubai and other GCC regions.

Right Angle

A right angle is made by two rays that meet at a vertex at 90°. This means the two rays need to be perpendicular to each other. The right angle is therefore referred to as 90-degree angle.

Contact us